Бейне: Ромбтың диагональдары бір-бірін екіге бөлетінін қалай дәлелдейсің?
2024 Автор: Lynn Donovan | [email protected]. Соңғы өзгертілген: 2023-12-15 23:49
Ішінде барлығы ромб қабырғалары тең, ал қарама-қарсы қабырғалары параллель. Әрі қарай а ромб сонымен қатар параллельграмм болып табылады, сондықтан а қасиеттерін көрсетеді параллелограмм және бұл Параллелограммның диагональдары бір-бірін екіге бөледі.
Сәйкесінше ромбтың диагональдары бір-бірін екіге бөле ме?
Кез келгенінде ромб , the диагоналдар (қарсы бұрыштарды байланыстыратын сызықтар) бір-бірін екіге бөледі тік бұрыштарда (90°). Бұл, әрбір диагональ кеседі басқа екі тең бөлікке бөлінеді және олардың қиылысу бұрышы әрқашан 90 градус болады. Жоғарыдағы суретте кескінді өзгерту үшін кез келген шыңды сүйреңіз ромб және бұл солай екеніне өзіңізді сендіріңіз.
Екіншіден, ромб диагональдары перпендикуляр ма? А-ның қасиеттері Ромб The диагоналдар болып табылады перпендикуляр бір-біріне және екіге бөлу. Көршілес бұрыштар қосымша болып табылады (мысалы, ∠A + ∠B = 180° үшін). А ромб Бұл параллелограмм кімдікі диагоналдар болып табылады перпендикуляр бір біріне.
Осыны ескере отырып, ромбтың диагональдары перпендикуляр биссектрисалар екенін қалай дәлелдейсіз?
Дәлелдеу бұл ромбтың диагональдары перпендикуляр Жоғарыдағылардың жалғасы дәлел : Конгруентті үшбұрыштардың сәйкес бөліктері сәйкес, сондықтан барлық 4 бұрыштары (ортасында орналасқандар) тең. Бұл олардың барлығы 90 градусқа тең екендігіне әкеледі және диагоналдар болып табылады перпендикуляр бір біріне.
Ромб параллелограмм ба?
АНЫҚТАМА: А ромб Бұл параллелограмм төрт жағы сәйкес келеді. ТЕОРЕМА: Егер а параллелограмм Бұл ромб , әрбір диагональ жұп қарама-қарсы бұрыштарды екіге бөледі. ТЕОРЕМА Керісінше: Егер а параллелограмм Қарама-қарсы бұрыштарды екіге бөлетін диагональдары бар, ол а ромб.
Ұсынылған:
Шаршының диагональдары тең бе?
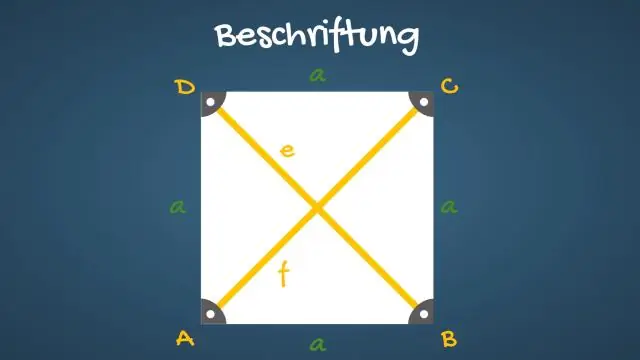
Шаршының диагональдары оның бұрыштарын екіге бөледі. Шаршының қарама-қарсы қабырғалары параллель және ұзындығы бірдей. Шаршының барлық төрт қабырғасы тең. Шаршының диагональдары тең
Параллелограмның екі диагональдары тең бе?
Параллелограммды екі үшбұрышқа бөлгенде, біз ортақ қабырғасының (мұнда диагональ) көлденең бұрыштары тең екенін көреміз. Бұл параллелограммдағы қарама-қарсы бұрыштардың да тең екендігін дәлелдейді. Параллелограмның диагональдарының ұзындығы бірдей емес
Екіге арналған префикс дегеніміз не?
Ағылшын тілінен алынған bi- префикстері және оның грек тіліндегі di- екеуі де «екі» дегенді білдіреді. Бұл «екі» префикстер жиі қолданылады, әсіресе би-. Жиі қолданылатын ағылшын тіліндегі bi- префиксінен бастайық, ол «екі» дегенді білдіреді. Велосипедтің «екі» дөңгелегі бар
AutoCAD бағдарламасында сызықты қалай екіге бөлуге болады?
Мынаны орындау керек: Пәрмен жолында Break сөзін теріңіз немесе үзіліс құралын таңдаңыз. Бұзғыңыз келетін жолды таңдаңыз. F теріңіз (бірінші нүкте үшін), Enter. Қайдан теріңіз және Енгізіңіз, ығысуды бастағыңыз келетін нүктені таңдаңыз, содан кейін қашықтықты теріңіз, мысалы, @12,0, Enter
Бір байтта неше бит бар бір байтта неше бит бар?
Екілік сандағы әрбір 1 немесе 0 бит деп аталады. Осыдан 4 биттен тұратын топ ниббл деп аталады, ал 8 бит байт жасайды. Байттар - екілік жүйеде жұмыс істегенде өте кең таралған сөз